You are watching a preview-version of the website. Click here to log out.

About
News
Products & Services
Guidelines
Contact
Browse Publications By Name
Browse Publications By Subject

From Pythagoras to Fourier and From Geometry to Nature

Next Chapter in Book

DOI: https://doi.org/10.55060/b.p2fg2n.ch008.220215.011

Chapter 8. Pseudo-Chebyshev Functions

Downloads:
1,764
Full-Text Views:
116

Starting from the rhodonea curves of integer indices, passing from polar to Cartesian coordinates, we find the connection with the first kind Chebyshev polynomials. However, the rhodoneas exist even in the case of fractional indices. This led to the idea of the existence of an analytic theory that extends these polynomials to the case of fractional indices. In this way, we obtain mathematical entities which, although no longer polynomials, continue to verify some of the properties of the above-mentioned Chebyshev polynomials and were therefore called pseudo-Chebyshev functions (PCF in short) of the first kind.

We start by considering the pseudo-Chebyshev functions of the first and second kind, which are an extension of these kind of Chebyshev polynomials to the case of fractional indices. We put by definition:

Tpq(x)=cos(pq arccos(x)) 
1−x2 Upq(x)=sin(pq arccos(x)) 
where p and q are integers and q ≠ 0. Note that Definitions (8.1) and (8.2) hold even for negative indices, that is for p/q < 0, according to the parity properties of the trigonometric functions.

Note that these functions arise naturally, extending to the fractional indices the corresponding polynomials of the first and second kind.

8.1 Basic Properties of the First and Second Kind PCF

We recall here only a few properties of these functions, but many others have been proven in several recent articles [6, 23, 24, 77, 82]. The following theorems hold:

Theorem 8.1.

The pseudo-Chebyshev functions Tpq(x) satisfy the recurrence relation:

Tpq+1(x)=2 x Tpq(x)−Tpq−1(x) 

Proof. Write Equation (8.3) in the form:

Tpq+1(x)+Tpq−1(x)=2 x Tpq(x) 

Then use Definition (8.1) and the trigonometric identity:

cosα+cosβ=2 cos(α+β2) cos(α−β2)

Theorem 8.2.

The pseudo-Chebyshev functions Upq(x) satisfy the recurrence relation:

Upq+1(x)=2 x Upq(x)−Upq−1(x) 

Proof. Write Equation (8.4) in the form:

Upq+1(x)+Upq−1(x)=2 x Upq(x) 

Then use Definition (8.2) and the trigonometric identity:

sinα+sinβ=2 sin(α+β2) cos(α−β2)

8.2 The Case of Half-Integer Degree

We now consider the case of the half-integer degree, which seems to be the most interesting one, since the resulting pseudo-Chebyshev functions satisfy the orthogonality properties in the interval (−1, 1) with respect to the same weights of the corresponding Chebyshev polynomials [24].

Definition. For any integer k:

Tk+12(x)=cos((k+12) arccos(x)) 1−x2 Uk−12(x)=sin((k+12) arccos(x)) 1−x2 Vk+12(x)=cos((k+12) arccos(x)) Wk+12(x)=sin((k+12) arccos(x)) 

Note that the above definition holds even for k + 1/2 < 0, taking into account the parity properties of the circular functions. We will show that, in the case of half-integer degree, the pseudo-Chebyshev functions satisfy not only the recursion analogues to the classical ones, but even the orthogonality properties.

8.2.1 Orthogonality of the First and Second Kind PCF

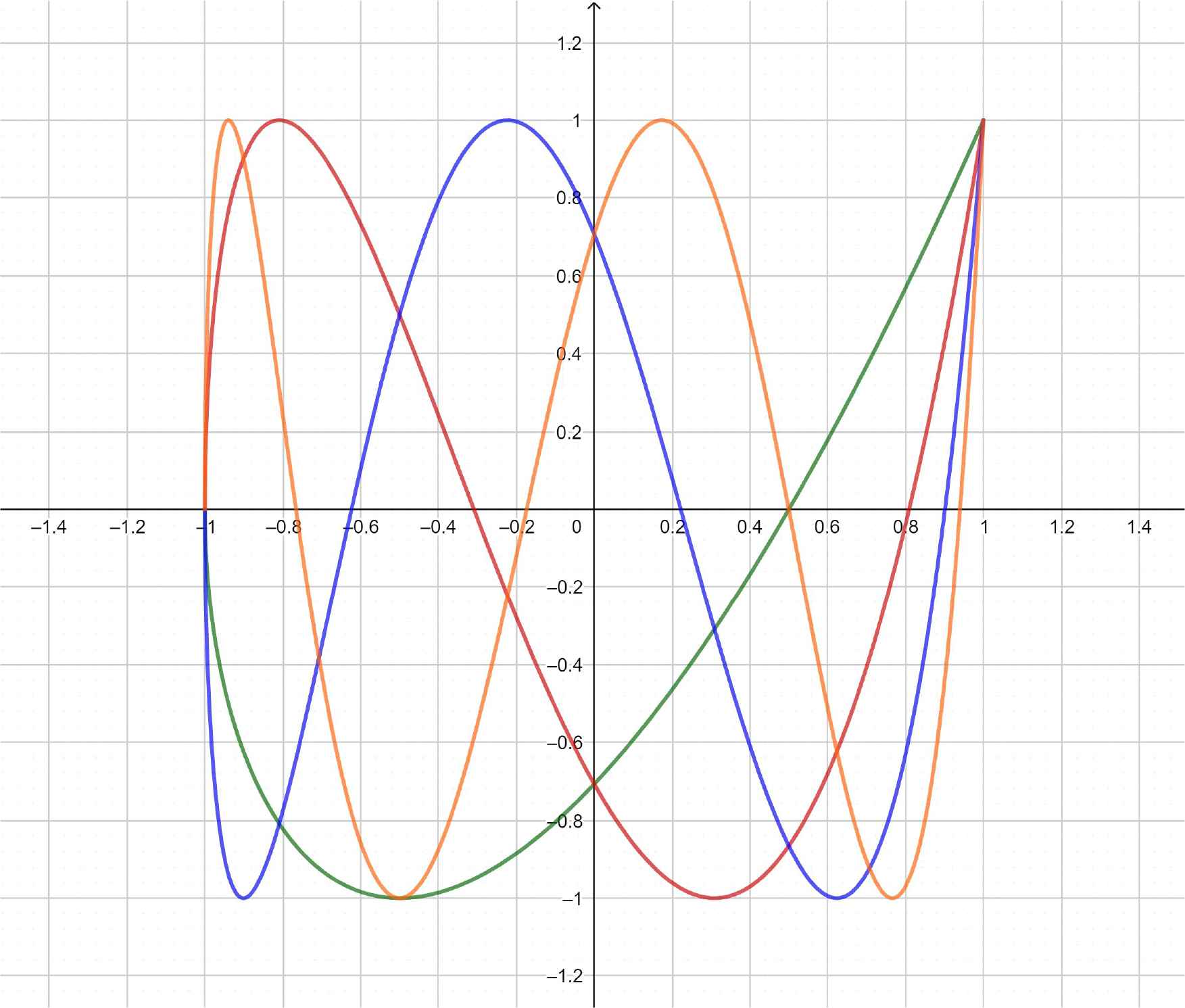
A few graphs of the Tk+12 functions are shown in Figure 15.

Figure 15

Tk+1/2(x), k = 1 (green), 2 (red), 3 (blue), 4 (orange).

Theorem 8.3.

The pseudo-Chebyshev functions Tk+1/2(x) satisfy the orthogonality property:

∫−11Th+12(x) Tk+12(x)11−x2 dx=0   (h≠k) 
where h, k are integers,
∫−11Tk+122(x)11−x2 dx=π2

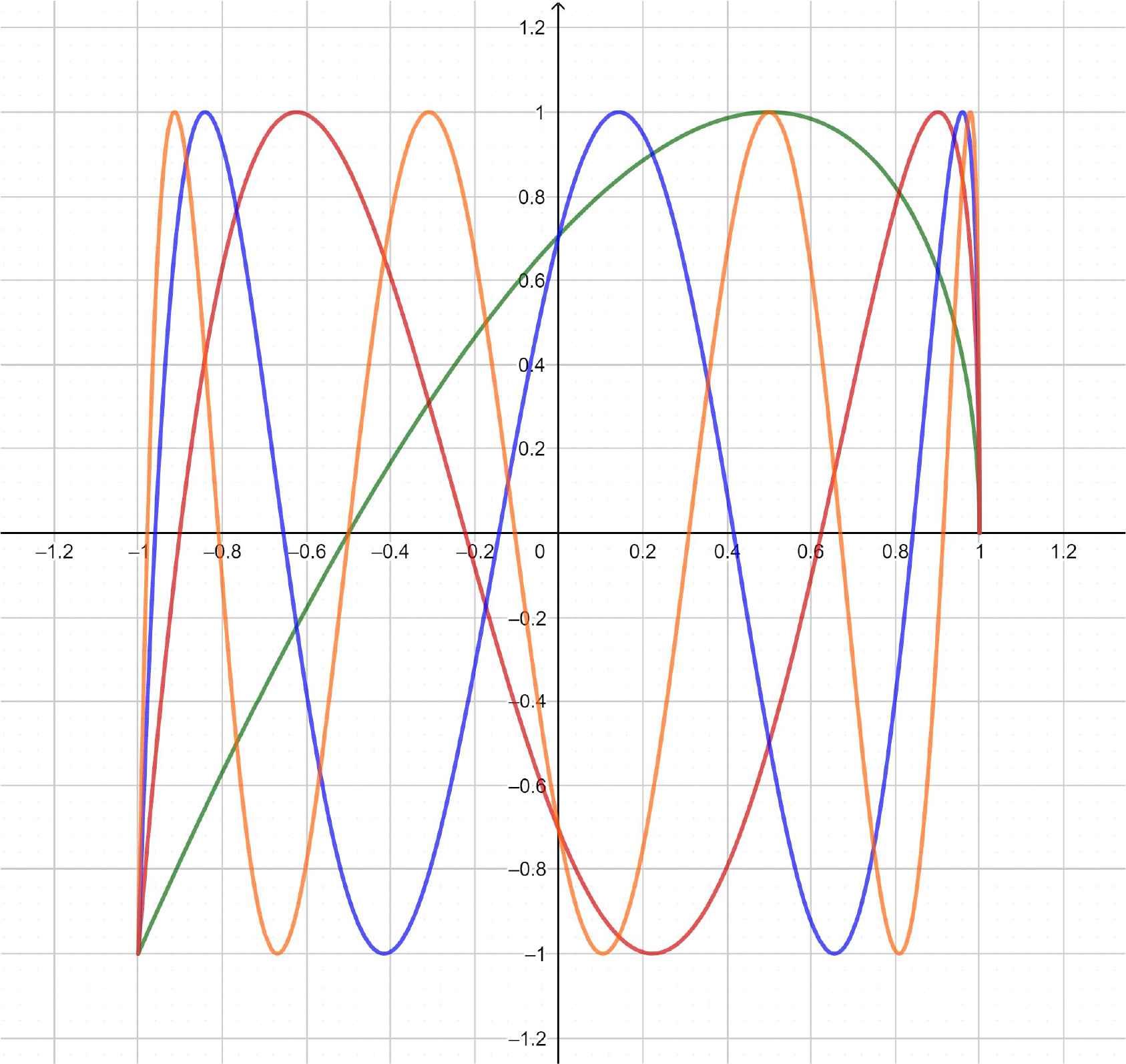
A few graphs of the Uk+12 functions are shown in Figure 16.

Figure 16

Uk+1/2(x), k = 1 (green), 2 (red), 3 (blue), 4 (orange).

Theorem 8.4.

The pseudo-Chebyshev functions Uk+12(x) satisfy the orthogonality property:

∫−11Uh+12(x) Uk+12(x)1−x2 dx=0   (h≠k) 
where h, k are integers,
∫−11Uk+122(x) 1−x2 dx=π2 

Proof. We prove only Theorem 8.3 since the proof of Theorem 8.4 is similar. From the Werner formulas, we have:

∫−11cos[(h+12)arccos(x)] cos[(k+12)arccos(x)]11−x2 dx =2 ∫0π/2cos[(2h+1)t]cos[(2k+1)t] dt=0 
and
∫−11cos2[(k+12)arccos(x)]11−x2 dx=2 ∫0π/2cos2((2k+1)t) dt=π2

8.3 Basic Properties of the Third and Fourth Kind PCF

The third kind pseudo-Chebyshev functions (Figure 17) satisfy the recurrence relation:

{Vk+12(x)=2 x Vk−12(x)−Vk−32(x) V± 12(x)=12 (1−x) 

Figure 17

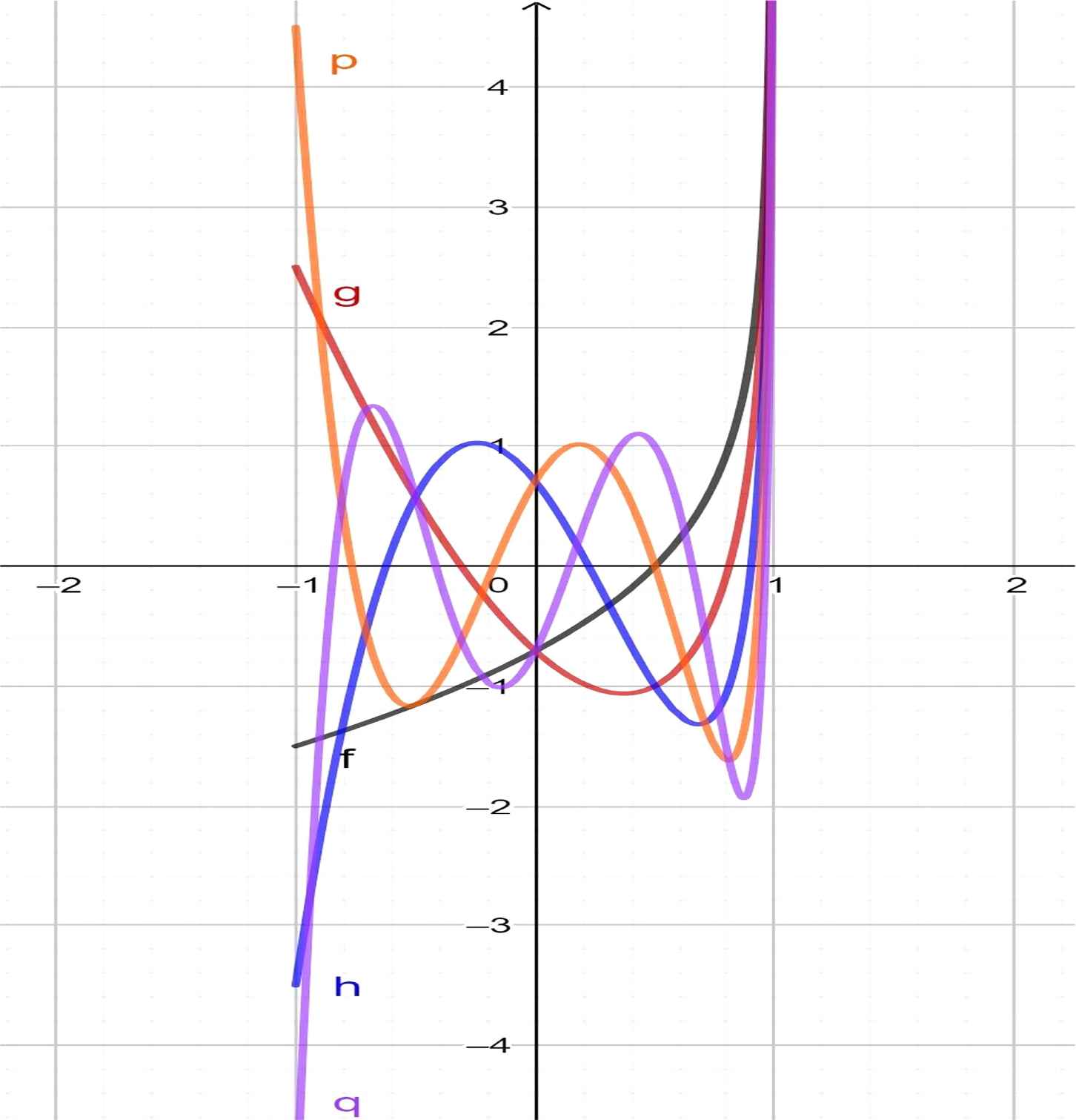
Vk+1/2(x), k = 1 (grey), 2 (red), 3 (blue), 4 (orange), 5 (violet).

The orthogonality property holds:

∫−11Vh+12(x) Vk+12(x) 1−x2 dx=0   (h≠k)
∫−11Vk+122(x) 1−x2 dx=π2

The fourth kind pseudo-Chebyshev functions (Figure 18) satisfy the recurrence relation:

{Wk+12(x)=2 x Wk−12(x)−Wk−32(x) W± 12(x)=±1−x2 

Figure 18

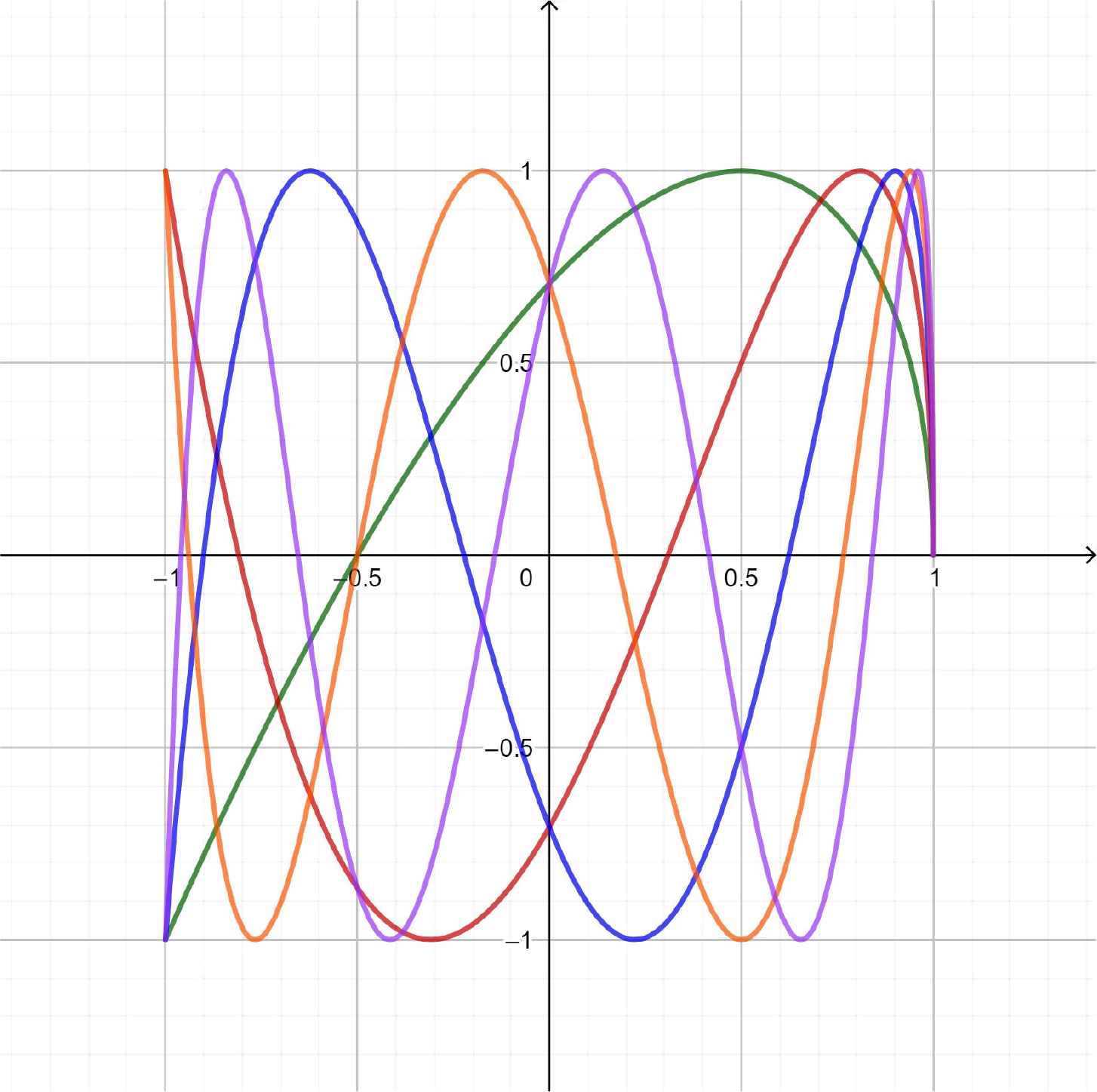
Wk+1/2(x), k = 1 (green), 2 (red), 3 (blue), 4 (orange), 5 (violet).

The orthogonality property holds:

∫−11Wh+12(x) Wk+12(x) 11−x2 dx=0   (h≠k) 
and furthermore:
∫−11Wk+122(x) 11−x2 dx=π2 

Remark 2.

More technical properties such as the hypergeometric representations [93], location of zeros, differential equations, Rodrigues-type formulas, etc. are reported in [23].

Next Chapter in Book